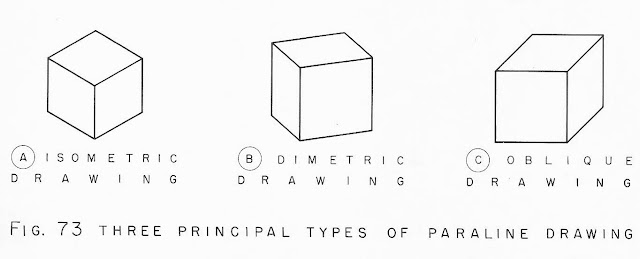
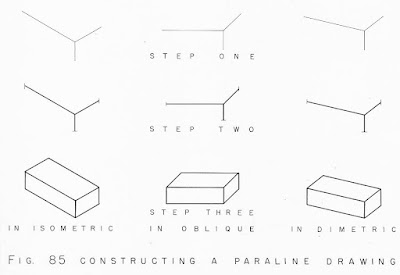
Paraline Drawings (Axonometric Projections)
Our options for creating the illusion of three-dimensional depth upon a two-dimensional surface typically involves one of the following two options:
1) Linear Perspective: parallel lines of objects and forms create the illusion of depth by converge towards one or more vanishing points. There is one fixed point of view and line of sight.
2) Paraline Drawings (Axonometric Projection): Parallel lines of objects and forms create the illusion of depth without converging towards a vanishing point. There is an infinitely scalable point of view and line of sight.
Paraline drawing is what most drawing students do accidentally when they attempt to draw a form that has parallel edges and is receding in space (such as a rectangular table, model stand, etc). They know both ends of the table are in fact the same size and they draw them as such. However, once they measure and compare two parallel edges (one closer and one farther away) they will see very readily that, from their particular fixed point of view, the further edge is in fact smaller than the closer edge. There is a conflict between what they know (the object in question is right and true and the furthest edge should be the same dimension as the closer edge if only they they could walk right up to each side and measure them) and what they see (the front edge is actually a greater than the back edge from their fixed point of view).
 |
| A student drawing that appears more like a paraline drawing than a perspective drawing. This is an extremely common quality with beginning, and some advanced, drawing students. |
Because of this often seen conflict in student drawings, it's very important to know at least a bit about what paraline drawing is so that the student can compare their efforts to it. Are they actually doing paraline drawing when in fact they are attempting a linear perspective drawing? This is a blog post all about paraline drawing and it's many permutations - it can get a little confusing I know. The big takeaway is that each of the following types of projections use parallel lines to create depth and that unlike linear perspective, these lines do not converge towards a vanishing point. See my other posts if you are looking for information on linear perspective.
The above images were scanned from the book Design Graphics by C. Leslie Martin, 1962. I found the drawings in the book so satisfying that I decided to scan them and post them here.









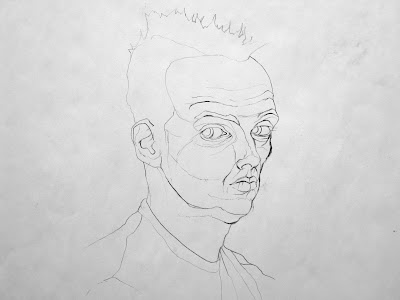
%20-drawing_detail1494.jpg)
Comments